今から約４０００年前の紀元前２０００年頃のエジプトには縄張り師（地面師やヤクザではない）という人達がいて、農地や建物を建てる時に測量などを行っていたそうです。その時に必要となるのが正しい直角を作り出すことです。今回はその方法の説明です。

又、紀元前１８００年頃のメソポタミア地方でも同じような考え方で直角を作りだしていたそうです。
彼等が行っていた直角を作り出す方法は以下のとおりです。

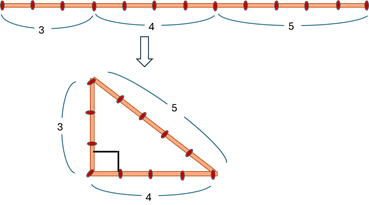
長い真っ直ぐなロープに端から端まで等間隔に結び目を１３個作ります。
そのロープの結び目を頼りに、長さ３、４、５の所で折り曲げて三角形を作ります。
すると長さ３と４の辺の間の角度が直角になるという訳です。　
3^２＋４^２＝５^２（三平方の定理）

この三平方の定理の証明は約１５００年後の古代ギリシャのピタゴラス（紀元前５８２年―紀元前４９６年）によりなされました、故にピタゴラスの定理とも言われていますね。